Linear Search:

Definition:

Linear Search is a sequential search algorithm in which a list or array's elements are traversed sequentially until the required element is discovered; if not, the search continues until the end of the data set.

Time Complexity:

1. Best Case:

• The element being searched could be found in the first position.
• In this case, the search ends with a single successful comparison.
• Thus, the best-case for linear search algorithm is O(1).

2. Average Case:

• When the element searched is in the middle of the array/list, the average case of the Linear Search Algorithm is O(n).

3. Worst Case:

• The element being searched may be at the last position in the array/list or not at all. For both of which the search will continue until the end.
• Thus, in the worst-case scenario of the linear search algorithm is O(n).

Space Complexity:

• The linear search algorithm takes up no extra space; its space complexity is O(1) for an array of n elements.

Application of Linear Search Algorithm:

• Linear search can be applied to both single-dimensional and multi-dimensional arrays.
• Linear search is easy to implement and effective when the array contains only a few elements.
• Linear Search is also efficient when the search is performed to fetch a single search in an unordered-List.

Example in Javascript:

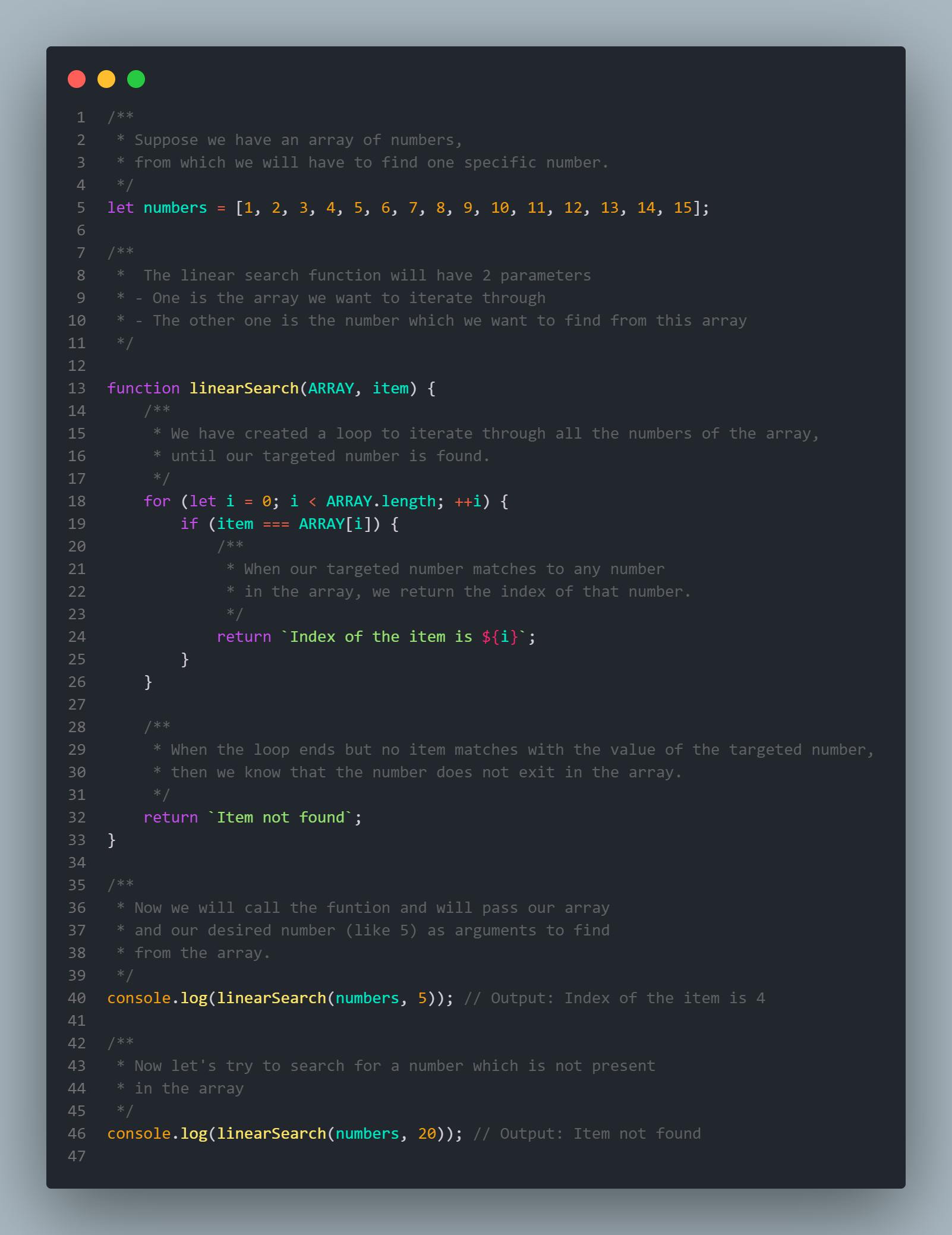
Why linear search is not efficient?

There is no denying the ease of linear search. However, because it evaluates each element separately, it takes time and is consequently ineffective. A linear search method might become quite time-consuming if we needed to identify a number out of, say, 1,000,000 numbers and that number was in the last spot.