Time and Space Complexity

👉 Time Complexity

What is Time complexity?

The time complexity of an algorithm quantifies the amount of time taken by an algorithm to run as a function of the length of the input. Note that the time to run is a function of the input and not the actual execution time of the machine on which the algorithm is running.

Why Time and Space complexity are important?

An algorithm is a limited series of precise instructions that are often carried out by a computer to complete a task. The efficiency of an algorithm may be determined by its space and time complexity. Even if we are aware that there are several approaches to a given problem in programming, understanding how an algorithm operates effectively might improve our performance. Knowing how to analyze a program or algorithm using space and time complexity can cause the program to behave in the desired optimal conditions.

Different types of Time Complexities

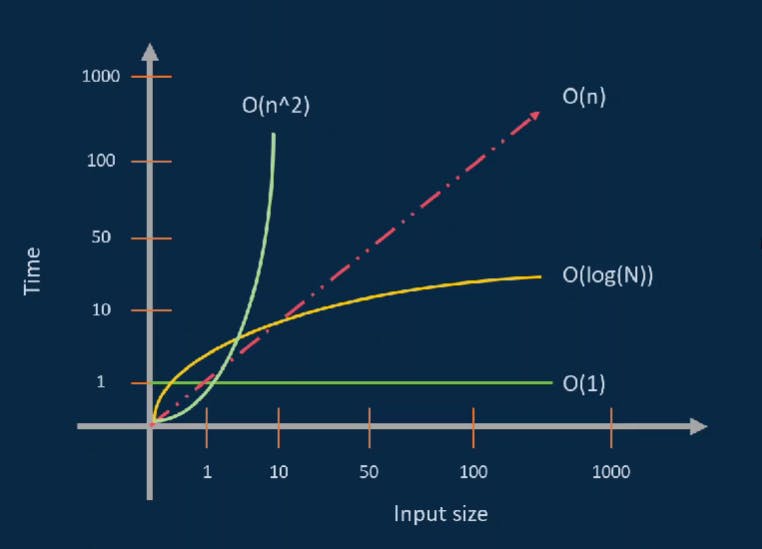
Time Complexity is given by time as a function of the length of the input. And a relation exists between the input data size (n) and the number of operations performed with respect to time. This relation is denoted as O(n), where "O" is the order of growth and "n" is the length of the input. It is also known as "Big O Notation".

There are different types of time complexities. They are:

1. Constant Time - O(1)
2. Linear Time - O(n)
3. Logarithmic Time - O(log n)
4. Quadratic Time - O(n^2)
5. Cubic Time - O(n^3) and so on.

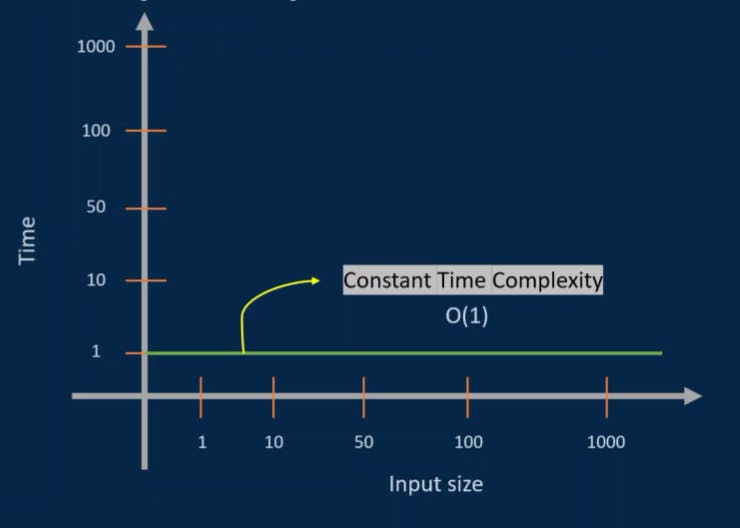
Constant Time - O(1)

The algorithm that has a time complexity of O(1) does not depend on the input size n. Whatever the input size may be, the runtime will always be the same.

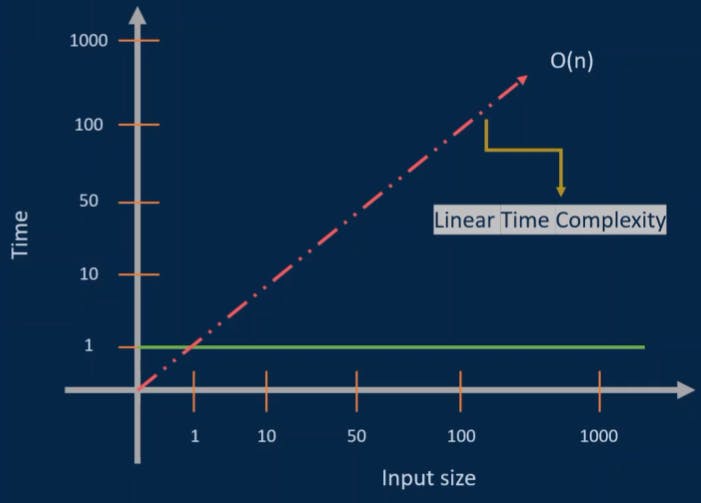
Linear Time - O(n)

The algorithm has a linear time complexity when its run time increases linearly with the length of the input. Algorithms such as Linear Search have this kind of time complexity.

Logarithmic Time - O(log n)

The algorithm that lowers the amount of the input data in each step has a logarithmic time complexity. This shows that the number of operations and the input size are not equal. As the input size grows, the number of operations decreases. Algorithms such as Binary Search have logarithmic time complexity.

Quadratic Time - O(n^2)

When the execution time of an algorithm grows non-linearly(n2) with the length of the input, the algorithm is said to have a non-linear time complexity. Algorithms with this level of time complexity include Bubble Sort.

• A graph of the time complexities are shown below:

How should we calculate time complexity?

Any operations like assignment and comparison operators will take 1 unit of time which is represented as O(1).

Example-1

let a = 10,
    b = 20;
let c = a + b;
console.log(c); //30

Here,

Assignment Operations: 3 units O(3)
Arithmetic Operations: 1 unit  O(1)
Total Time Complexity: 4 units i.e. O(3)+O(1) = O(4)

Here, the total complexity will be O(1) instead of O(4). Here, a and b are our inputs. Even if their values are increased, the overall time complexity will not be affected. This is because the time complexity of our program is not dependent on the length of our input. Thus, O(1) is also known as constant time complexity.

Example-2

let sum = 0,
    n = 10;

for (let i = 1; i <= n; ++i) {
    sum += i;
}

Here we can see a loop that is depended on n. When n = 10, then the loop will run 10 times; if n = 100 then the loop will run 100 times. We know the time required to run will increase if number of loops is increased. So the time complexity of this code is O(n).

Time complexity calculation

Time Complexity != Execution Time

For example: The time a code will take to run using a super computer will take way less time than to run the same code using general computers.

Then what does time complexity actually mean? It means how time grows depends upon the input size.

• To calculate time complexity we have to see two things. They are:
  ✅ Avoid Constants
  ✅ Avoid small values

Example-3

function run(n) {
    /*
     * Here we can there is a nested for loop
     * Thus the time complexity will be O(n^2)
     */
    for (let i = 1; i <= n; ++i) {
        for (let j = 1; i <= n; j++) {
            // code.
        }
    }

    /*
     * Here we can there is only one for loop
     * Thus, the time complexity will be O(n)
     */
    for (let k = 1; i <= n; ++i) {
        console.log(k);
    }
}

run(10);

Thus, the total time complexity of the code is O(n^2 + n). Here, n is smaller than n^2. Thus the time complexity will be O(n2). The reason small values are avoided is that in the overall time complexity they do not mean much. For example, if n = 100 then n^2 = 10000, here can see a big difference. The difference will be even more when the value of n is increased.

✔️ Let's take a look at an exercise below:

Exercise-1: What will be the time Complexity of 5n^3 + 3n^2 + n + 10?

= 5n^3 + 3n^2 + n + 10
= n^3 + n^2 + n (At first, we remove the constants and coefficients)
= n^3 (Then we remove the small values)

Thus, the total time complexity is n^3

Difference between good and bad time complexity

• Let us take 3 popular time complexities O(n^2), O(n) and O(log n).

• Let 1 unit time = O(1) = 1ms

• If n = 10^4 then the total run time will be:

Here, we can see the huge time difference between the three. Amongst the three, O(n^2) time complexity is the worst and O(log n) performed the best.

👉 Space Complexity

What is Space Complexity?

Space complexity is a way to establish an approximate relationship between the size of input data and primary memory used by the algorithm to produce the expected result. It is closely correlated with how much input the algorithm receives. Simply calculating how much space the variables in an algorithm occupy will yield the space complexity. The algorithm runs more quickly the less space it needs. It's also crucial to understand that space difficulty and time complexity are unrelated.

Why Time Complexity is more important than Space Complexity?

Reusing space or memory is simple. Easy memory expansion is possible. On the other hand, it is difficult to reduce the amount of time required for computation. Although parallelization helps, it cannot make the program's serial portion run more quickly. Practically speaking, we are currently able to take advantage of inexpensive memory while yet craving faster computers.

Note: If one does not need to worry about how fast software operates and has a limited amount of memory to dedicate to the software then we will give more priority to space complexity to make our software.

Conclusion

In this blog, we covered the fundamentals of time complexity and the reasons for its necessity for the algorithms we create. Finally, we learned how to determine the order of notation for any algorithm based on the cost function and the number of times the statement is defined to execute. We also saw what different sorts of time complexities are used for different kinds of functions.

Wrap Up

Thank you for reading.

If you find this helpful, leave a like, share, and follow me, at @srafsan to read more articles.